Prog1-Part2

本文最后更新于 2026年2月7日下午

感觉自己下半学期学的有点问题，写点笔记复习一下

感觉下半学期的重点是编译原理，主要可以分为这么几个部分：

Lexer: 把程序转化为Token
Parser: 把Token转化为语言的数据类型
Elaborator: 静态类型检查
Evaluator: 求值

自我感觉1.3.4.掌握的还行，Paser还是有点不明白。

以及3.4.的Derivation Tree还要再记一下表示方法。

编译原理这一块还是先拿课上的顺序进行整理：3.4.1.2.

编译原理

Elaborator——静态类型检查

作为人类，可能能一步一步推导类型，但怎么让计算机做呢？

仔细观察（bushi），可以抽象出来几条规则，这里拿latex抄一遍：

渲染有问题，直接用图片了QwQ

这个还是比较好理解的，因为不涉及环境的变更，一点一点推导下去就可以了。

Evaluator——动态求值

这里涉及环境的变更，所以语法上有些地方要注意。

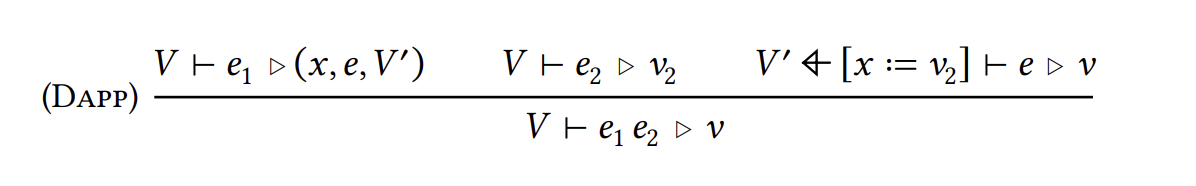
函数要写成Tuple的形式
新的环境要在最后表示出来

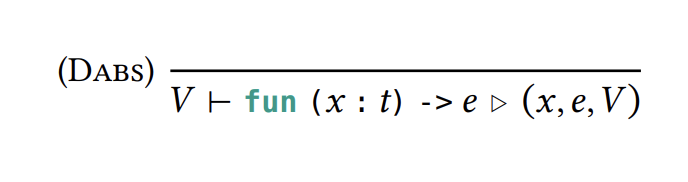
函数在Abs时候要写成Tuple形式。

Lexer——Token化

这个没啥难的，直接字符串explode后match就可以

Parser——把Token处理为Eval和Elab能处理的形式

这里用的是Recursively Descending Parser
主要思想就是先处理优先级低的，然后一步一步向下处理。
这里用到了OCaml一个制造相互使用的函数的语法糖：and。
就是可以前面先用这个函数，然后and 函数名=…补上。

以及一般的函数形式都是一个Tuple，前面放处理好，已经表示为语言本身类型的Token，后面放待处理的Token。

一个Prog1自定义的helper函数：

let expect t =function
| t' :: tr when t' = t -> tr
| ts -> failwith (expect_msg ("'" ^ string_of_token t ^ "'") ts)

同理，我们也能写出处理变量的helper函数：

1
2
3

let var = function
|VAR x :: ts ->(x,ts)
|ts->failwith ...

它的基本功能是如果List的下一个是想要的元素，那么把满足要求的元素删掉，返回剩下的。如果不是就failwith。

处理FUN和IF的时候，这种嵌套的关键字时，这个函数就十分有用。因为正如上面所说，Tuple的snd存的是待处理元素。而IF后面的ELSE和THEN都没有match，因此肯定会成为“剩下的”，此时就可以用expect接收并接着处理。

同理，FUN的处理也是这样。一步一步匹配LP,COL,RP,ARR。

最终就能解析出exp了。

解决了符号嵌套什么的问题，我们就可以进一步完善我们的exp部分了。

Recursive Descendent Paser

一个核心思想是在type representation里，用[]option bracket来制造un-deterministic:

\begin{aligned} ty::=&pty[\text{->}ty]\\ pty::=&Bool|Int|(ty) \end{aligned}

这里复习一下我一分不得的Mini Test题目：

type token=HE|HO|LP|RP|SIM
;;
type exp=He|Ho|Sim of exp*exp
;;
type cexp ts=
match pty ts with
| t1, SIM :: ts = let t2,ts = cexp ts in (Sim(t1,t2),ts)
| p->p
and pty = function
| HE::ts -> (He,ts)
| HO::ts -> (Ho,ts)
| LP::ts -> 
        let t1,ts = cexp ts in
        let ts = expect RP ts in
        (t1,ts)
| _->failwith "Not Valid"

核心还是每次解析的时候尝试看看下层还有没有可以解析的，然后一层一层向下。

核心就是Grammar，对每个非终结符总结一个替换方式然后按优先级逐个应用。

然后一个完整的paser最后还要加一个函数包装一下：

1
2
3

let paser ts=match cexp ts with
|(e,[])->e
|ts->failwith ...

这样的意思是解析成功就返回paser结果，不行就报错。

形式化的递归表达

现在课上在讲这个，顺手写一下吧。

递归式的一种表示方法

e.g.

$Fib(x) = \text{IF } x<2 \text{ THEN } x \text{ ELSE } Fib(x-1)+Fib(x-2)$

可以表示为 $\text{IF } x<2 \text{ THEN } \langle\rangle \text{ ELSE } \langle x-1,x-2\rangle$

递归关系

刚才的柿子中， $\langle\rangle$ 中的东西叫Precedent Argument. 如果我们把当前参数和Precedent Argument中间连一条有向边，就构成的一个递归关系R。

可以和之前的Termination Relation联系起来：你能terminate，这个递归才能结束。怎么判断能否Terminate呢，看这个function能不能在某种encoding下countable。

证明函数定义和数学上的函数表达的是一个东西

这一部分主要是数学上的证明，跟编程知识就没啥关系了。

但是minitest里给出了需要的证明方式：

1.证明Dom something $\subseteq$ Dom f

给出Termination Function，证明两个Dom都对这个function terminate，所以有这个关系

2.证明数学上一致

对每个条件分支，做一下和Mathematical induction类似的变形。

Structural Induction

Given a claim, for each possible arg, make the claim a induction form.

解题过程的注意事项

首先，起手式是固定的，以List相关内容为例：

Let $X$ be an arbitrary yet fixed type, we show the $\forall xs\in \mathcal{L}(X), ys\in \mathcal{L}(X),...\text{(the claim) by structural induction on } xs$

重点是arbitrary but fixed以及全称量词的使用.
然后开始induction，先证基本类型，再证induction的part。
重点就是要写得尽可能详细，每一步都要有出处，常见的有：

arithmetic
a=b+c
IH(induction hypothesis)
Definition of function
…

Prog1的time complexity

Size function revisited

注意这个东西的选择。如果你给一个 $\mathcal{O}(n)$ 算法选择了形如 $\lambda n\in \mathbb{N},2^n$ 的size function，那么你在主定理的柿子里就要用形如 $T(n)=T(2^{\log_2n-1})+\mathcal{O}(\text{something})$ 的柿子。
感觉这里的“Size”指的是输入规模。

主定理复习

对于形如

T(n)=b\cdot T(\frac{n}{a})+\mathcal{O}(n^d\log^s n)

f(n)=n^d\log^s n

的柿子，有：

$a<b^d, \mathcal{O}(n^d\log^s n)$
$a=b^d,\mathcal{O}(n^d\log^{s+1}n)$
$a>b^d,\mathcal{O}(n^{\log_b a})$

在Prog1里， $T(n)$ 被替换成了 $t\space n$ 的形式， $f(n)$ 被替换成了 $co\space n$ 的形式。做题的时候要小心一点。

解题格式

在mini test中给出：

写出size function。
写出主定理的形式。
给出复杂度。

Ocaml中的Imperative Programming

从Ref开始

首先是几个和Ref相关的符号：

1
2
3

let x=ref 0; (*创建一个指向放着‘0’这个值的内存地址的指针*)
let a=!x;    (*取出这个地址里的变量并赋值*)
x:=3;        (*更新内存里的值*)

有了内存，我们就能进一步考虑数组操作了：

(* 注意，OCaml的数组是0-index *)
let arr1=Array.make 100 0;; (*创建一个n个cell，值全为val的数组*)
let arr2=Array.init 100 (fun a->a+1);;  (*创建一个n个cell，i从0到n-1，第i个cell值为 f(i)*)
arr1.(0)<-100;; (*赋值操作*)
arr1.(0);; (*取值操作*)
(*一种前缀和的fold_left写法*)
let pre arr=
    Array.fold_left (fun acc curr->let ()=
    arr.(snd(acc))<-fst(acc)+curr in
    (fst(acc)+curr,snd(acc)+1)) (0,0) arr;;

对应的Minitest内容为：

求前缀和
Generator：每次调用给出一个新值：e.g. 不断调用fac，出1,1,2,6,24,…
读代码填空。注意所有跟着“;”的内存操作对于最后的值都是不影响的，只需要看最后那个值的值和类型。

期末复习

考试做题策略

感觉得按简单到难的顺序来做，我认为是这样的：

时间复杂度
数学表达和Induction Proof
Imperative Programming
Concrete and Dynamic Syntax

接下来分专题记录一下不明白的一些点

数学相关

Recursion Relation

它是以集合形式表达的。
并且只考虑recursion的分支，如：

f(x,y)=\begin{cases} 1,\quad y=0\\ 3,\quad y=1\\ f(x-4,y-1)+f(x-2,y-2),\quad y>1 \end{cases}

的Recursion Relation是

R=\{((x,y),(x',y'))|x\in \mathbb{Z}\land y\in\mathbb{N}\land y>1\land (x',y')\in\{(x-2,y-2),(x-4,y-1)\}\}

首先，Recursion Relation可以理解为一张DAG的边的描述，因此｜前的部分肯定是一个pair，代表边的表示。
后面部分先定义了x,y的值域，代表在这个情况下才能做recursion。
然后再描述下一次recursion的参数。
这样一个Recursion Relation就写完了

Correctness Theory

就像之前所记录的，分为两部分完成。

首先，我们对不是lambda的那个函数找一个termination function，这样就可以说明它可以对所有argument terminate，也就代表它的值域就是参数值域的笛卡尔积，也就能说明这两个东西的Dom相等。
然后，我们通过对定义的函数的变形来证明这是这么个东西。

Inductive Proof

感觉核心还是

n的选择，一般是 $n=k+1, k\in\mathbb{N}$
Arbitrary, 所有在inductive case中会变的，没有指明arbitrary的，都需要提一嘴。
IH一般都是 $\forall$ something, 一个关系。

有一个作业题很有意思，是直接对n进行reduction进行不下去，因此转而证一个更强的结论。

List Reduction

一些常用原因：

Definition of $|\cdot|$
Associativity/Commutativity

Time Complexity

证明工具

这是证明题能用的几个结论

\mathcal{O}(f n)=\mathcal{O}(c\cdot fn+gn), \mathcal{O}(g)\subseteq\mathcal{O}(f)

和形如

\mathcal{O}(n)\subseteq\mathcal{O}(n\log n)

Function和Specification

函数的Big O：是结果的。

函数的Specification的：是一步一步算出来的过程的。这个是一般理解上的Time Complexity.

主定理

记住关键是 $a$ 和 $b^d$ 之间的关系，见之前的复习部分

Imperative Programming

熟记二分写法

一道例题： $\mathcal{O}(\log n)$ 找出有序数组中某个值出现的区间，按数组index的闭区间。
实现：

let search_range arr tg = 
    let find_fst arr tg=
        let rec pos l r = 
            if (l>r) then None
            else let m = (l+r)/2 in
            let y = arr.(m) in
            if (tg<y) then pos l (m-1)
            else if (tg>y) then pos (m+1) r else
            if (m=0||arr.(m-1)<y) then Some m
            else pos l (m-1) 
        in pos 0 (Array.length arr - 1)
    in
    let find_lst arr tg=
        let rec pos l r = 
            if (l>r) then None
            else let m = (l+r)/2 in
            let y = arr.(m) in
            if (tg<y) then pos l (m-1)
            else if (tg>y) then pos (m+1) r else
            if (m=Array.length arr-1 ||arr.(m+1)>y) then Some m
            else pos (m+1) r 
        in pos 0 (Array.length arr - 1)
    in
    (find_fst arr tg,find_lst arr tg)
            ;;

这里的代码还没有需要用到ref，感觉那个是generator那一块的内容。

Generator

这里有两种写法。一种是定义全局ref,另一种是定义时用一堆let ... in来定义，两种是等价的。

几个小技巧：

因为OCal在一段用";"隔开的表达式中会取最后一个值作为整个柿子的值。因此想做到先返回值再副作用就要先拿一个局部变量捕获一下然后再修改，返回。
OCaml允许你重新组合已有操作符，然后写出对应定义成为新的运算符，因此尽量不要连写运算符。
时刻牢记Right Associative。例子如下：
1
let map_gen f g ()= f (g());;
如果你想写一个每次调用输出f处理后的generator值，那么你得把g()包起来

Generator实现的时候一定要把主要的生成逻辑部分放到函数里，因为这是它的Mutability的来源。如果写死就固定了，就成原汁原味的函数式编程了。注意下面这段代码里的fun ()->...

let int_lst lst =
 if List.length lst =0 then
     failwith "Not valid";
 let h = ref lst in
 let t = ref [] in fun ()->
 ((if !h = [] then 
     (h:=List.rev !t;
     t:=[]);
     (match !h with 
     | x::xr->t:=x::!t;h:=xr;x()
     |_->failwith "Possible?"))
 )

OCaml里的副作用好像也是基于Expression的，因此可以有以下类比
- 圆括号块->大括号块
- 分号->分号
- 最后一个expression->这一段的return value
没要求你复杂度别乱优化，舒服就行。（指List的@运算符该用就用）

Signature

模块分为两种。一种是Sig，纯定义，一种是struct，是实现。

Sig开头如下:

module A = sig
type xd
val init : int -> int
...
end

struct 开头如下：

module a : A = struct 
type xd=int
val init b = b+100
...
end

这里冒号A的作用是规定这个a struct的实现的实现里面必须要有A里的所有的定义。
以及实现和定义都不需要分隔符，直接写就行。

编译原理部分

Paser

尝试写一遍

type token=HE|HO|LP|RP|SIM
;;
type exp=He|Ho|Sim of exp*exp
;;
let cexp t1 = 
match pty ts with
| t1, SIM::ts -> let t2, ts = cexp ts in  (Sim(t1,t2),ts)
| p->p and pty = function
| HE::ts -> (He,ts)
| HO::ts -> (Ho,ts)
| SIM::ts -> let t1,ts = cexp ts in
            let ts = expect RP ts in
            (t1,ts)
| _->failwith "possible?"
;;
let paser ty = match cexp ty with
| (t,[]) -> t
| ts ->failwith "something"

Rules

#函数式编程

Prog1-Part2

https://chenxizhou233.github.io/posts/622f6855.html

作者

Xizhou Chen

发布于

2026年1月8日

许可协议

MathI 上一篇

ITCS 下一篇

Prog1-Part2

编译原理

Elaborator——静态类型检查

Evaluator——动态求值

Lexer——Token化

Parser——把Token处理为Eval和Elab能处理的形式

Recursive Descendent Paser

形式化的递归表达

递归式的一种表示方法

递归关系

证明函数定义和数学上的函数表达的是一个东西

1.证明Dom something⊆\subseteq⊆Dom f

2.证明数学上一致

Structural Induction

解题过程的注意事项

Prog1的time complexity

Size function revisited

主定理复习

解题格式

Ocaml中的Imperative Programming

从Ref开始

期末复习

考试做题策略

数学相关

Recursion Relation

Correctness Theory

Inductive Proof

List Reduction

Time Complexity

证明工具

Function和Specification

主定理

Imperative Programming

熟记二分写法

Generator

Signature

编译原理部分

Paser

Rules

1.证明Dom something $\subseteq$ Dom f